quarta-feira, 13 de novembro de 2013
segunda-feira, 4 de novembro de 2013
Geometria Analítica
A geometria analítica foi um estudo realizado pelo matemático René Descartes que aliou os conhecimentos da álgebra ao estudo das figuras geométricas. No entanto, antigamente a geometria analítica era conhecida como Geometria de coordenadas e geometria cartesiana, pois com a aplicação da álgebra na geometria é possível fazer qualquer representação geométrica por meio de pares ordenados, equações e inequações.
SISTEMA CARTESIANO ORTOGONAL
Se duas retas se cruzam e formam um ângulo de 90º elas são perpendiculares. A perpendicularidade dessas duas retas forma um sistema cartesiano ortogonal.
As duas retas são chamadas de eixos:
Eixo das abscissas: reta x.
Eixo das coordenadas: reta y.
Onde as retas x e y se encontram é formado um ponto, que é chamado de ponto de origem.
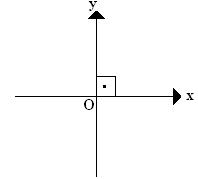
O sistema cartesiano ortogonal é dividido em quatro partes e cada uma é um quadrante.
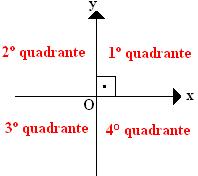
Um ponto no sistema cartesiano ortogonal é formado por dois pontos, um do eixo das abscissas e outro do eixo das ordenadas.
O ponto no sistema cartesiano ortogonal é chamado de par ordenado.
.jpg)
O ponto X possui um número x que é a abscissa do ponto P.
O ponto Y possui um número y que é a ordenada do ponto P.
(x, y) é chamado de par ordenado do ponto P.
Portanto, para determinarmos um ponto P no sistema cartesiano ortogonal é preciso que as abscissas e as ordenadas sejam dadas.
Veja o sistema cartesiano ortogonal abaixo e os pontos que estão indicados.
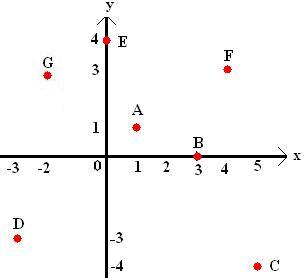
O ponto A (1, 1) encontra-se no 1° quadrante.
O ponto B (3, 0) encontra-se no eixo das abscissas x.
O ponto C (5, -4) encontra-se no 4º quadrante.
O ponto D (-3, -3) encontra-se no 3º quadrante.
O ponto E (0, 4) encontra-se no eixo das ordenadas
O ponto F (4, 3) encontra-se no 1º quadrante.
O ponto G (-2, 3) encontra-se no 2° quadrante.
DISTÂNCIA ENTRE DOIS PONTOS
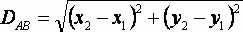
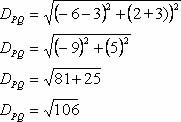
.jpg)
.jpg)
.jpg)
.jpg)
SISTEMA CARTESIANO ORTOGONAL
Se duas retas se cruzam e formam um ângulo de 90º elas são perpendiculares. A perpendicularidade dessas duas retas forma um sistema cartesiano ortogonal.
As duas retas são chamadas de eixos:
Eixo das abscissas: reta x.
Eixo das coordenadas: reta y.
Onde as retas x e y se encontram é formado um ponto, que é chamado de ponto de origem.
O sistema cartesiano ortogonal é dividido em quatro partes e cada uma é um quadrante.
Um ponto no sistema cartesiano ortogonal é formado por dois pontos, um do eixo das abscissas e outro do eixo das ordenadas.
O ponto no sistema cartesiano ortogonal é chamado de par ordenado.
.jpg)
O ponto X possui um número x que é a abscissa do ponto P.
O ponto Y possui um número y que é a ordenada do ponto P.
(x, y) é chamado de par ordenado do ponto P.
Portanto, para determinarmos um ponto P no sistema cartesiano ortogonal é preciso que as abscissas e as ordenadas sejam dadas.
Veja o sistema cartesiano ortogonal abaixo e os pontos que estão indicados.
O ponto A (1, 1) encontra-se no 1° quadrante.
O ponto B (3, 0) encontra-se no eixo das abscissas x.
O ponto C (5, -4) encontra-se no 4º quadrante.
O ponto D (-3, -3) encontra-se no 3º quadrante.
O ponto E (0, 4) encontra-se no eixo das ordenadas
O ponto F (4, 3) encontra-se no 1º quadrante.
O ponto G (-2, 3) encontra-se no 2° quadrante.
DISTÂNCIA ENTRE DOIS PONTOS
A distância entre dois pontos é determinada pela Geometria Analítica, responsável por estabelecer relações entre fundamentos geométricos e algébricos. As relações são intituladas com base num sistema de coordenadas cartesianas, que é constituído de dois eixos perpendiculares enumerados.

No plano cartesiano, qualquer ponto possui uma coordenada de localização, basta identificar o ponto e observar os valores primeiramente em relação ao eixo horizontal x (abscissa) e posteriormente em relação ao eixo vertical y (ordenada).
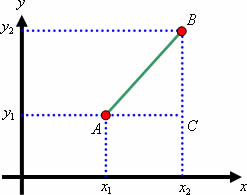
Nesse sistema de coordenadas podemos demarcar dois pontos e determinar a distância entre eles. Observe:

Observe que o triângulo formado é retângulo de catetos AC e BC e hipotenusa AB. Se aplicarmos o Teorema de Pitágoras nesse triângulo determinando a medida da hipotenusa estaremos também calculando a distância entre os pontos A e B. Vamos aplicar as propriedades da relação de Pitágoras no triângulo ABC, originando a expressão matemática responsável pela determinação da distância entre dois pontos em função de suas coordenadas.
O Teorema de Pitágoras diz: “A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”. No triângulo ABC temos que:
Cateto AC = x2 – x1
Cateto BC = y2 – y1
Cateto BC = y2 – y1
Exemplo 1
Qual a distância entre os pontos P(3, –3) e Q(–6, 2)?
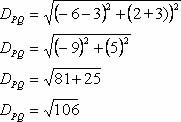
A distância entre os pontos P e Q é igual a √106 unidades.
COORDENADA DO PONTO MÉDIO DE UM SEGMENTO DE RETA
O segmento de reta possui inúmeros pontos alinhados, mas somente um deles irá dividir o segmento em duas partes iguais. A identificação e a determinação do ponto médio de um segmento de reta será demonstrado com base na ilustração a seguir.
.jpg)
O segmento de reta AB terá um ponto médio (M) com as seguintes coordenadas (xM, yM). Observe que os triângulos AMN e ABP são semelhantes, possuindo os três ângulos respectivamente iguais. Dessa forma, podemos aplicar a seguinte relação entre os segmentos que formam os triângulos. Veja:
.jpg)
Podemos concluir que AB = 2 * (AM), considerando que M é o ponto médio do segmento AB. Temos:
.jpg)
xP – xA = 2*(xM – xA)
xB – xA = 2*(xM – xA)
xB – xA = 2xM – 2xA
2xM = xB – xA + 2xA
2xM = xA + xB
xM = (xA + xB)/2
Utilizando método análogo, conseguimos demonstrar que yM = (yA + yB )/2.
Portanto, considerando M o ponto médio do segmento AB, temos a seguinte expressão matemática capaz de determinar a coordenada do ponto médio de qualquer segmento no plano cartesiano:
xB – xA = 2*(xM – xA)
xB – xA = 2xM – 2xA
2xM = xB – xA + 2xA
2xM = xA + xB
xM = (xA + xB)/2
Utilizando método análogo, conseguimos demonstrar que yM = (yA + yB )/2.
Portanto, considerando M o ponto médio do segmento AB, temos a seguinte expressão matemática capaz de determinar a coordenada do ponto médio de qualquer segmento no plano cartesiano:
.jpg)
Percebemos que o cálculo da abscissa xM é a média aritmética entre as abscissas dos pontos A e B. Assim, o cálculo da ordenada yM é a média aritmética entre as ordenadas dos pontos A e B.
CONDIÇÃO DE ALINHAMENTO DE TRÊS PONTOS.
Com três pontos distintos e não alinhados formamos um plano, para que com eles seja formada uma reta é preciso que eles estejam alinhados.
Considere os pontos A(1,2), B(3,0), C(4,-1). Colocando-os em um plano cartesiano percebemos que a união irá formar uma reta, ou seja, eles estão alinhados.

Unir os três pontos distintos em um plano cartesiano é uma opção para verificar seu alinhamento, mas isso nem sempre apresenta uma resposta segura, pois um dos três pontos pode estar milímetros fora da reta formada, o que deixa os três pontos não alinhados.
Por esse motivo, ao verificar se os três pontos são alinhados, é preciso seguir a seguinte condição:
Os pontos A, B e C pertencem à reta formada acima e o ponto B é comum aos segmentos AB e BC, nesse caso podemos aplicar a seguinte propriedade: Duas retas paralelas que possuem um ponto em comum são coincidentes.
Unindo essa propriedade com o cálculo dos coeficientes, iremos concluir que os pontos A, B e C serão paralelos se o coeficientes dos dois segmentos mAB e mBC forem iguais.
mAB = 0 – 2 = - 2 = - 1
4 – 3 2
MBC = -1 – 0 = -1 = - 1
4 – 3 1
Como mAB = mBC podemos dizer que os três (A, B e C) pontos estão alinhados.
Analisando esse exemplo chegamos à seguinte condição de alinhamento de três pontos:
Dado três pontos distintos A (xA, yB), B (xB,yB) e C (xC, yC), eles serão alinhados se, somente se, os coeficientes mAB e mBC forem iguais.
Considere os pontos A(1,2), B(3,0), C(4,-1). Colocando-os em um plano cartesiano percebemos que a união irá formar uma reta, ou seja, eles estão alinhados.
Unir os três pontos distintos em um plano cartesiano é uma opção para verificar seu alinhamento, mas isso nem sempre apresenta uma resposta segura, pois um dos três pontos pode estar milímetros fora da reta formada, o que deixa os três pontos não alinhados.
Por esse motivo, ao verificar se os três pontos são alinhados, é preciso seguir a seguinte condição:
Os pontos A, B e C pertencem à reta formada acima e o ponto B é comum aos segmentos AB e BC, nesse caso podemos aplicar a seguinte propriedade: Duas retas paralelas que possuem um ponto em comum são coincidentes.
Unindo essa propriedade com o cálculo dos coeficientes, iremos concluir que os pontos A, B e C serão paralelos se o coeficientes dos dois segmentos mAB e mBC forem iguais.
mAB = 0 – 2 = - 2 = - 1
4 – 3 2
MBC = -1 – 0 = -1 = - 1
4 – 3 1
Como mAB = mBC podemos dizer que os três (A, B e C) pontos estão alinhados.
Analisando esse exemplo chegamos à seguinte condição de alinhamento de três pontos:
Dado três pontos distintos A (xA, yB), B (xB,yB) e C (xC, yC), eles serão alinhados se, somente se, os coeficientes mAB e mBC forem iguais.
INCLINAÇÃO DE UMA RETA E O SEU COEFICIENTE ANGULAR
Determinamos uma reta no plano cartesiano conhecendo dois pontos distintos, mas também é possível ser determinada conhecendo apenas um ponto e um ângulo, pois uma reta s intercepta o eixo Ox em um ponto M formando um ângulo α.
O ângulo α é formado pela reta r e por um ponto do eixo Ox localizado à direita do ponto M. A sua medida irá variar entre 0°≤ α < 180°.
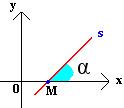
Esse ângulo é a inclinação da reta e a sua tangente é o valor do seu coeficiente angular. Sendo que só será possível encontrar o seu coeficiente angular quando a reta não for vertical, ou seja, o valor de α deverá ser diferente de zero.
Exemplo 1:
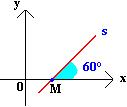
Inclinação da reta s igual a 60º.
Coeficiente angular igual a m = tg 60° = √3.
Exemplo 2:
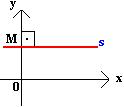
Inclinação da reta s igual a 0°, pois é paralela ao eixo Ox.
Coeficiente angular igual a m = tg0º = 0.
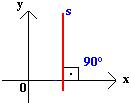
Inclinação da reta é igual a 90°.
Não terá como encontrar o valor do coeficiente angular da reta s quando a inclinação for igual a 90°, pois não é possível encontrar o valor da tangente de 90°.
O ângulo α é formado pela reta r e por um ponto do eixo Ox localizado à direita do ponto M. A sua medida irá variar entre 0°≤ α < 180°.
Esse ângulo é a inclinação da reta e a sua tangente é o valor do seu coeficiente angular. Sendo que só será possível encontrar o seu coeficiente angular quando a reta não for vertical, ou seja, o valor de α deverá ser diferente de zero.
Exemplo 1:
Inclinação da reta s igual a 60º.
Coeficiente angular igual a m = tg 60° = √3.
Exemplo 2:
Inclinação da reta s igual a 0°, pois é paralela ao eixo Ox.
Coeficiente angular igual a m = tg0º = 0.
Inclinação da reta é igual a 90°.
Não terá como encontrar o valor do coeficiente angular da reta s quando a inclinação for igual a 90°, pois não é possível encontrar o valor da tangente de 90°.
Créditos : Marcos Noé, Danielle de Miranda.
Variância (V) e Desvio Padrão (DP)
A variância tem o objetivo de analisar o grau de variabilidade de determinadas situações, através dela podemos perceber desempenhos iguais, muito próximos ou muito distantes. A média aritmética pode ser usada para avaliar situações de forma geral, já a variância determina de forma mais específica as possíveis variações, no intuito de não comprometer os resultados da análise. Vamos, através de um exemplo, determinar a eficiência da variância.
Observe as notas de três competidores em uma prova de manobras radicais com skates.
Competidor A: 7,0 – 5,0 – 3,0
Competidor B: 5,0 – 4,0 – 6,0
Competidor C: 4,0 – 4,0 – 7,0
Ao calcular a média das notas dos três competidores iremos obter média cinco para todos, impossibilitando a nossa análise sobre a regularidade dos competidores.
Partindo dessa ideia, precisamos adotar uma medida que apresente a variação dessas notas no intuito de não comprometer a análise.
Observe os cálculos:
Competidor A
VA = (7-5)² + (5-5)² + (3-5)² = 4+0+4 = 2,667
3 3
Competidor B
VB = (5-5)² + (4-5)² + (6-5)² = 0+1+1 = 0,667
3 3
Competidor C
VC = (4-5)² + (4-5)² + (7-5)² = 1+1+4 = 2
3 3
Desvio Padrão
É calculado extraindo a raiz quadrada da variância.
Competidor A
√2,667 = 1,633
Competidor B
√ 0,667 = 0,817
Competidor C
√2 = 1,414
Competidor A
√2,667 = 1,633
Competidor B
√ 0,667 = 0,817
Competidor C
√2 = 1,414
Tabelas de Frequências
A frequência absoluta, ou apenas frequência, de um valor é o número de vezes que uma determinada variável assume esse valor. Ao conjunto das frequências dos diferentes valores da variável dá-se o nome de distribuição da frequência (ou apenas distribuição).
A frequência relativa, é a percentagem relativa à frequência.
A frequência acumulada de um valor, é o numero de vezes que uma variável assume um valor inferior ou igual a esse valor.
A frequência relativa acumulada, é a percentagem relativa à frequência acumulada.
A tabela de frequências é uma forma de representação da frequência de cada valor distinto da variável. Juntamente com as frequências, esta poderá incluir frequências relativas, frequências acumuladas e frequências relativas acumuladas.
Consideremos a seguinte tabela
Assim a tabela de frequências da variável Sexo será:
A frequência relativa, é a percentagem relativa à frequência.
A frequência acumulada de um valor, é o numero de vezes que uma variável assume um valor inferior ou igual a esse valor.
A frequência relativa acumulada, é a percentagem relativa à frequência acumulada.
A tabela de frequências é uma forma de representação da frequência de cada valor distinto da variável. Juntamente com as frequências, esta poderá incluir frequências relativas, frequências acumuladas e frequências relativas acumuladas.
Consideremos a seguinte tabela
| Nome | Sexo | ||
| Manuela | F | Giovane | M |
| Manuel | M | Pietro | M |
| Carol | F | Cristal | F |
| Marilia | F | Sonia | F |
| Jonas | M | Sueide | F |
Temos:
Sexo Masculino:
Frequência absoluta : (a quantidade de homens) = 4
Frequência relativa: ( a quantidade de homens multiplicado pelo total de pessoas) = 4 em 10 = 40%
Sexo Feminino:
Frequência absoluta : (a quantidade de mulheres) = 6
Frequência relativa: (a quantidade de mulheres pelo total de pessoas) = 6 em 10 = 60%
Assim a tabela de frequências da variável Sexo será:
variável
|
freq. absoluta (n)
|
freq. relativa (%)
|
| Sexo | ||
| M | 4 | 40% |
| F | 6 | 60% |
| Total | 10 | 100% |
Assinar:
Postagens (Atom)