Ponto Médio

Segmento de reta é limitado por dois pontos de uma reta. Por exemplo, considere a reta r e dois pontos A e B que pertencem a essa reta.



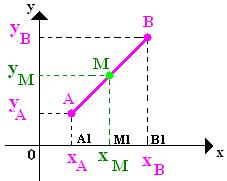
A distância dos pontos A e B é o segmento da reta r.

Por ser um “pedaço” de uma reta podemos medir o seu comprimento (distância entre dois pontos de uma reta), assim possuindo seu ponto médio (ponto que separa o segmento ao meio).

O segmento de reta possui inúmeros pontos alinhados, mas somente um deles irá dividir o segmento em duas partes iguais.

O segmento de reta AB terá um ponto médio (M) com as seguintes coordenadas (xM, yM). Observe que os triângulos AMN e ABP são semelhantes, possuindo os três ângulos respectivamente iguais. Dessa forma, podemos aplicar a seguinte relação entre os segmentos que formam os triângulos. Veja:

considerando M o ponto médio do segmento AB, temos a seguinte expressão matemática capaz de determinar a coordenada do ponto médio de qualquer segmento no plano cartesiano:

Percebemos que o cálculo da abscissa xM é a média aritmética entre as abscissas dos pontos A e B. Assim, o cálculo da ordenada yM é a média aritmética entre as ordenadas dos pontos A e B. 

Exemplo 1

Dadas as coordenadas dos pontos A(4,6) e B(8,10) pertencentes ao segmento AB, determine as coordenadas do ponto médio desse segmento.

xA = 4
yA = 6
xB = 8
yB = 10

xM = (xA + xB) / 2
xM = (4 + 8) / 2
xM = 12/2
xM = 6

yM = (yA + yB) / 2
yM = (6 + 10) / 2
yM = 16 / 2
yM = 8

As coordenadas do ponto médio do segmento AB é xM (6, 8). 

Exemplo 2

Dados os pontos P(5,1) e Q(–2,–9), determine as coordenadas do ponto médio do segmento PQ.

xM = [5 + (–2)] / 2
xM = (5 – 2) / 2
xM = 3/2

yM = [1 + (–9)] / 2
yM = (1 – 9) / 2
yM = –8/2
yM = –4

Portanto, M(3/2, –4) é o ponto médio do segmento PQ.